Un ángulo debe tener tres características: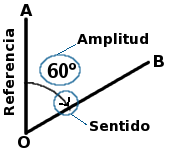

- Referencia: Desde dónde se mide.
- Amplitud: La magnitud medida del ángulo («el número» para ser más explícito).
- Sentido: A partir de la línea de referencia, hasta dónde se mide.
Los ángulos horizontales son una de las cinco mediciones que se realizan en topografía plana (Ver capítulo 2), dentro de ellos podemos encontrar:
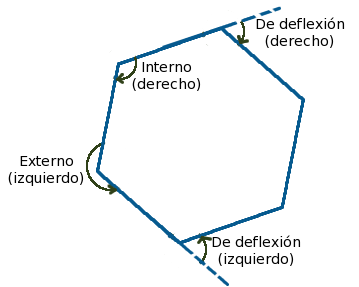
- Ángulos internos (en un polígono cerrado)
- Ángulos externos (en un polígono cerrado)
- Ángulos derechos (medidos en el sentido de las manecillas del reloj)
- Ángulos izquierdos (medidos en contra del sentido de las manecillas del reloj)
- Ángulos de deflexión (medidos desde la prolongación de una línea hasta la siguiente, pueden ser izquierdos o derechos)
Referencia
Para medir ángulos se pueden tomar tres tipos de líneas de referencia:
1. Magnética
Nuestro planeta está rodeado por un campo magnético cuyo origen es aún discutido. Se cree que se origina en las corrientes de la región ígnea de la Tierra, como consecuencia del movimiento de partículas cargadas eléctricamente, o, probablemente, son las corrientes de convección que se originan por el calor del núcleo. Quizás el campo magnético terrestre sea el producto de la combinación de las corrientes de convección con los efectos de la rotación terrestre.1

Sea cual sea su origen, el campo magnético de la Tierra ha tenido una importancia capital en la topografía, ya que hace que el planeta se comporte como un gran imán cuyo polo sur se encuentra al Norte del planeta y, por lo tanto, que el polo norte de una aguja imantada (brújula) señale desde cualquier parte hacia el Norte magnético de la Tierra, brindando una línea más o menos estable para tomar como referencia. Esa línea va a estar determinada por el punto desde el que se este realizando la observación (estación) y el Polo Norte Magnético.

Sea cual sea su origen, el campo magnético de la Tierra ha tenido una importancia capital en la topografía, ya que hace que el planeta se comporte como un gran imán cuyo polo sur se encuentra al Norte del planeta y, por lo tanto, que el polo norte de una aguja imantada (brújula) señale desde cualquier parte hacia el Norte magnético de la Tierra, brindando una línea más o menos estable para tomar como referencia. Esa línea va a estar determinada por el punto desde el que se este realizando la observación (estación) y el Polo Norte Magnético.
Los Polos Magnéticos se definen como el punto en la superficie de la Tierra donde las líneas del campo magnético son perpendiculares a la superficie terrestre. La mayoría de brújulas señalan el Polo Norte Magnético, que actualmente se ubica sobre territorio canadiense, cerca de 1 800 km al Sur del Polo Norte Geográfico.
El campo magnético de la Tierra está sujeto a variaciones seculares (a lo largo de las eras geológicas), anuales, e incluso diarias (también se producen inversiones magnéticas que consisten en cambio diametral de la posición de los polos magnéticos); razón por la cual en la actualidad no se utiliza extensamente la norte magnética como referencia en levantamientos de precisión.
2. Geográfica
Los Polos Geográficos de la Tierra se definen como los puntos en su superficie que se cortan con el eje de rotación del planeta.. El Norte Geográfico es usado con más frecuencia en la actualidad como referencia para medir ángulos, pues no presenta variaciones como las de los polos magnéticos, el inconveniente es que debe estar señalado con puntos establecidos con levantamientos de altísima precisión, o ser medido con GPS.
Este artículo es por ahora un esbozo, cuando tenga un tiempito lo termino, sin embargo, lo publico así porque lo que está escrito hasta ahora sirve como introducción. Gracias y disculpen la molestia. 
En vista de la acogida que ha tenido el artículo he decidido ampliarlo un poco más, en especial para dar respuesta a las preguntas de Estefanía Vera que aparecen en la sección de comentarios. Sin embargo, me voy a saltar un poco el orden para llegar a los temas que ella menciona. Toca esperar otro rato para que el artículo esté completo y bien estructurado. Les pido disculpas 
Rumbo
El rumbo de una línea es el ángulo horizontal agudo (<90°) que forma con un meridiano de referencia, generalmente se toma como tal una línea Norte-Sur que puede estar definida por el N geográfico o el N magnético (si no se dispone de información sobre ninguno de los dos se suele trabajar con un meridiano, o línea de Norte arbitraria).
Como se observa en la figura, los rumbos se miden desde el Norte (línea ON) o desde el Sur (línea OS), en el sentido de las manecillas del reloj si la línea a la que se le desea conocer el rumbo se encuentra sobre el cuadrante NOE o el SOW; o en el sentido contrario si corresponde al cuadrante NOW o al SOE.
Como el ángulo que se mide en los rumbos es menor que 90° debe especificarse a qué cuadrante corresponde cada rumbo.
Como se observa en la figura, los rumbos se miden desde el Norte (línea ON) o desde el Sur (línea OS), en el sentido de las manecillas del reloj si la línea a la que se le desea conocer el rumbo se encuentra sobre el cuadrante NOE o el SOW; o en el sentido contrario si corresponde al cuadrante NOW o al SOE.
Como el ángulo que se mide en los rumbos es menor que 90° debe especificarse a qué cuadrante corresponde cada rumbo.
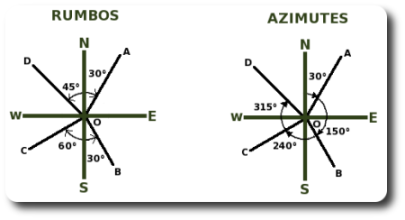
Por ejemplo en la figura las líneas mostradas tienen los siguientes rumbos:
| Línea | RUMBO |
| OA | N30°E |
| OB | S30°E |
| OC | S60°W |
| OD | N45°W |
Como se puede observar en la notación del rumbo se escribe primero la componente N o S del cuadrante, seguida de la amplitud del ángulo y por último la componente E o W.
Azimut
El azimut de una línea es el ángulo horizontal medido en el sentido de las manecillas del reloj a partir de un meridiano de referencia. Lo más usual es medir el azimut desde el Norte (sea verdadero, magnético o arbitrario), pero a veces se usa el Sur como referencia.
Los azimutes varían desde 0° hasta 360° y no se requiere indicar el cuadrante que ocupa la línea observada. Para el caso de la figura, las mismas líneas para las que se había encontrado el rumbo tienen el siguiente azimut:
Los azimutes varían desde 0° hasta 360° y no se requiere indicar el cuadrante que ocupa la línea observada. Para el caso de la figura, las mismas líneas para las que se había encontrado el rumbo tienen el siguiente azimut:
| Línea | AZIMUT |
| OA | 30° |
| OB | 150° |
| OC | 240° |
| OD | 315° |
Contra-rumbo y Contra-azimut (Rumbo o azimut inverso)
Cuando se desea conocer la dirección de una línea se puede ubicar un instrumento para medirla en cualquiera de sus puntos extremos, por lo tanto se llaman rumbo y azimut inversos a los observados desde el punto contrario al inicial. Para que quede más claro, si en el ejemplo de la figura se midieron primero los rumbos y azimutes desde el punto O (líneas OA, OB, OC y OD), el contra-rumbo y contra-azimut de cada línea corresponde a la dirección medida en sentido opuesto, desde cada punto hasta O (líneas AO, BO, CO y DO).
Cuando se trata de rumbos, para conocer el inverso simplemente se cambian las letras que indican el cuadrante por las opuestas (N <-> S y E <-> W). De manera que para la figura se tiene:
Cuando se trata de rumbos, para conocer el inverso simplemente se cambian las letras que indican el cuadrante por las opuestas (N <-> S y E <-> W). De manera que para la figura se tiene:
| Línea | RUMBO | CONTRA-RUMBO |
| OA | N30°E | S30°W |
| OB | S30°E | N30°W |
| OC | S60°W | N60°E |
| OD | N45°W | S45°E |
 Por el contrario, si se trata de azimutes, el inverso se calcula sumándole 180° al original si éste es menor o igual a 180°, o restándole los 180° en caso de ser mayor.
Por el contrario, si se trata de azimutes, el inverso se calcula sumándole 180° al original si éste es menor o igual a 180°, o restándole los 180° en caso de ser mayor.Contra-Azimut = Azimut ± 180°
Para la figura mostrada se observan los siguientes azimutes inversos:
| Línea | AZIMUT | CONTRA-AZIMUT |
| OA | 30° | 30°+180° = 210° |
| OB | 150° | 150°+180° = 330° |
| OC | 240° | 240°-180° = 60° |
| OD | 315° | 315°-180° = 135° |
Vale la pena volver a decir que en ningún caso un rumbo (o un rumbo inverso) puede ser mayor a 90°, ni un azimut (o contra-azimut) mayor a 360°.
Conversión de Rumbo a Azimut
Para calcular azimutes a partir de rumbos es necesario tener en cuenta el cuadrante en el que se encuentra la línea. Observando la figura anterior se puede deducir la siguiente tabla:
| Cuadrante | Azimut a partir del rumbo |
| NE | Igual al rumbo (sin las letras) |
| SE | 180° – Rumbo |
| SW | 180° + Rumbo |
| NW | 360° – Rumbo |
Se puede comprobar revisando los valores que aparecen en la figura.
Conversión de Azimut a Rumbo
Observando también la figura se ve que el cuadrante de la línea depende del valor del azimut así:
| Azimut | Cuadrante | Rumbo |
| 0° – 90° | NE | N ‘Azimut’ E |
| 90° – 180° | SE | S ‘180° – Azimut’ E |
| 180° – 270° | SW | S ‘Azimut – 180°’ W |
| 270° – 360° | NW> | N ‘360° – Azimut’ W |
Cálculo de Azimutes en poligonales
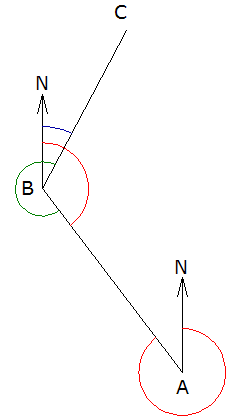 Una poligonal, sea abierta o cerrada, es una sucesión de distancias y direcciones (rumbo o azimut) formadas por la unión de los puntos en los que se armó el instrumento que se usó para medirlas (puntos de estación). Cuando se ubica el instrumento en una estación se puede medir directamente el azimut de la siguiente línea a levantar (si se conoce la dirección del N o si se “sostiene” el contra-azimut de la línea anterior), sin embargo, en ocasiones se mide el ángulo correspondiente entre las dos líneas que se intersectan en el punto de estación (marcando “ceros” en el ángulo horizontal del instrumento cuando se mira al punto anterior), a este último ángulo se le va a llamar “ángulo observado”.
Una poligonal, sea abierta o cerrada, es una sucesión de distancias y direcciones (rumbo o azimut) formadas por la unión de los puntos en los que se armó el instrumento que se usó para medirlas (puntos de estación). Cuando se ubica el instrumento en una estación se puede medir directamente el azimut de la siguiente línea a levantar (si se conoce la dirección del N o si se “sostiene” el contra-azimut de la línea anterior), sin embargo, en ocasiones se mide el ángulo correspondiente entre las dos líneas que se intersectan en el punto de estación (marcando “ceros” en el ángulo horizontal del instrumento cuando se mira al punto anterior), a este último ángulo se le va a llamar “ángulo observado”.Si el ángulo observado se mide hacia la derecha (en el sentido de las manecillas del reloj, que es el mismo en el que se miden los azimutes) se puede calcular el azimut de la siguiente línea con la siguiente expresión:
Azimut línea siguiente = Contra-azimut de la línea anterior + Ángulo observado
Se debe aclarar que si el resultado es mayor a 360° simplemente se le resta este valor.
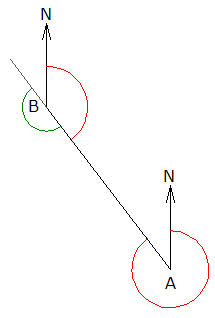
En la figura se observa que si el azimut conocido corresponde al de la línea AB (ángulo NAB en rojo), por lo tanto el contra-azimut es el ángulo NBA (también en rojo). El ángulo observado, medido en el sentido de las manecillas del reloj con el instrumento estacionado en el punto B es el ángulo ABC (en verde). El azimut que se desea conocer es el de la línea BC (ángulo NBC en azul). Por lo tanto se tiene la siguiente expresión:
Azimut BC = Contra-Azimut AB + Ángulo observado en B
Azimut BC =
Como es evidente que el resultado será mayor que 360° (en este caso en particular) entonces el azimut de la línea BC será:
Azimut BC = (
Esta expresión es válida sólo si el ángulo observado está medido en el mismo sentido del azimut (derecha), sin importar si es interno o externo.
Si se trata de calcular rumbos se pueden luego convertir los azimutes calculados de la forma anterior.
Notas
Bibliografía
Paul R. Wolf y Russel C. Brinker. Topografía. Novena Edición. Alfaomega. México, 1997



0 comentarios: